研究海洋流体动力学中多分数阶随机Davey–Stewartson方程（戴维–斯图尔特森方程）的精确解、灵敏度及混沌行为

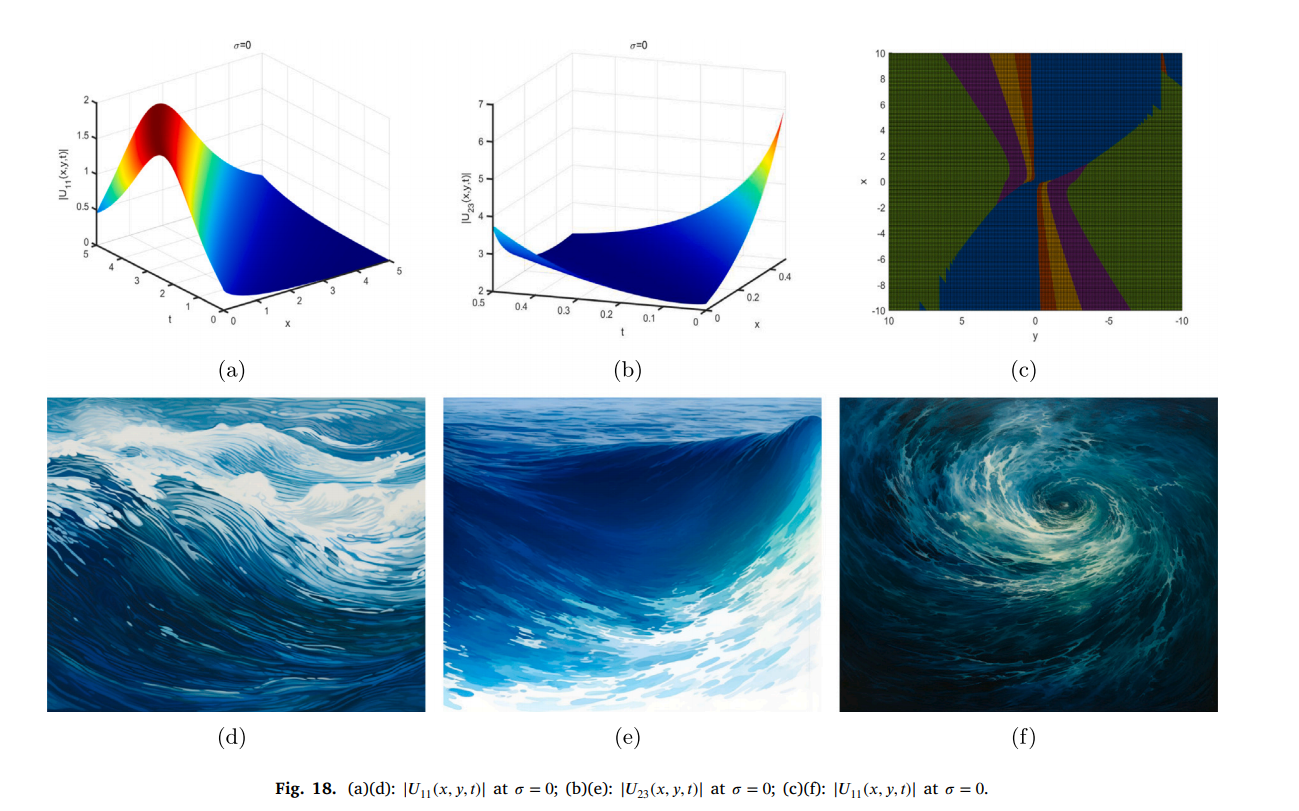
探索分数阶随机Davey-Stewartson方程（FDSDSE）的理论和应用研究，并在以下方面做出贡献：首先，团队发现了以前未知的FDSDSE精确解，包括Weierstrass椭圆函数解，为方程分析提供了新见解。其次，团队分析了噪声对随机解的影响，发现高噪声强度可能破坏模式，但乘法噪声能在一定程度上稳定解，这对研究海洋波动具有重要意义。第三，研究强调了导数阶数α对噪声动力学的影响，表明不同阶数的导数对噪声有不同作用，这对海洋研究人员选择适当导数以研究随机系统至关重要。第四，比较了不同”分数阶导数”对随机解中噪声的影响，发现适当的导数阶数能更准确描述海洋波浪行为，对改进波浪模型和预测海洋波浪具有重要意义。第五，研究了FDSDSE解中倾斜波变化的影响，观察到螺旋状图案，为理解海洋波浪传播提供了新见解。第六，通过敏感性分析和扰动因素探索了FDSDSE的相图和混沌行为，增强了对海洋水动力学研究的理解。最后，将研究结果与海洋中的已知波浪现象进行比较，突出了研究的实际相关性，为海洋科学和工程领域提供了有益启示。该研究成果2024年发表于Chaos, Solitons and Fractals杂志https://doi.org/10.1016/j.chaos.2024.114491 期刊为中国科学院SCI 1区杂志。作者顺序：戚建明（第一作者），崔青华（我校研究生），白雷强（我校研究生），孙逸群（唯一通讯作者）。上海电机学院为唯一完成单位。

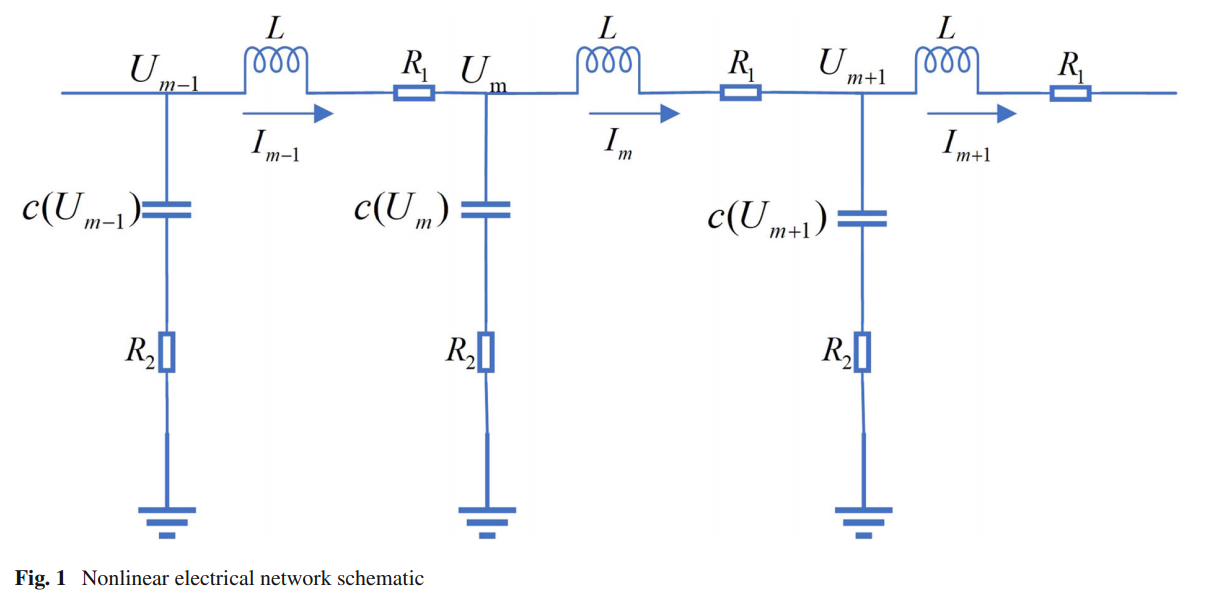
运用哈密顿动力学研究有损电力传输线模型中的分形与混沌行为

团队研究关于有损非线性电力传输线模型（LNETLM）突出了几个新颖的贡献：（1）引入了修正的$\frac{G}{G^2}$-扩展方法，该方法应用于具有贝塔导数的LNETLM，提供了以前未曾记录的精确孤子解；（2）通过广泛的计算机模拟，揭示了多种波动现象，如亮孤子、孤立孤子、抛物线孤子以及振荡奇异波，推动了对LNETLM中孤子传输波动动态的表征；（3）对比了相容性、M-截断导数、贝塔导数三种不同”分数阶导数”形式下中的贝塔导数在电力传输线系统建模中的独特优势；（4）将LNETLM方程转化为哈密顿系统，分析了相图、混沌现象和分形现象，增强了对系统动态和稳定性的理解；（5）拓展了对有损电力传输线模型的知识前沿，具有理论理解和信号传输及通信系统实际应用的意义。研究强调了脉冲状孤子在提升电信系统数据传输速率方面的潜力，预示着更高的效率和性能。该研究成果2024年发表于Nonlinear Dynamics杂志https://doi.org/10.1007/s11071-024-09981-2  期刊为中国科学院SCI 2区TOP杂志。作者顺序：戚建明（第一作者），王旭（我校研究生），孙逸群（唯一通讯作者）。上海电机学院为唯一完成单位。

分析多种分数阶随机Ginzburg-Landau方程中发生的分形和混沌行为

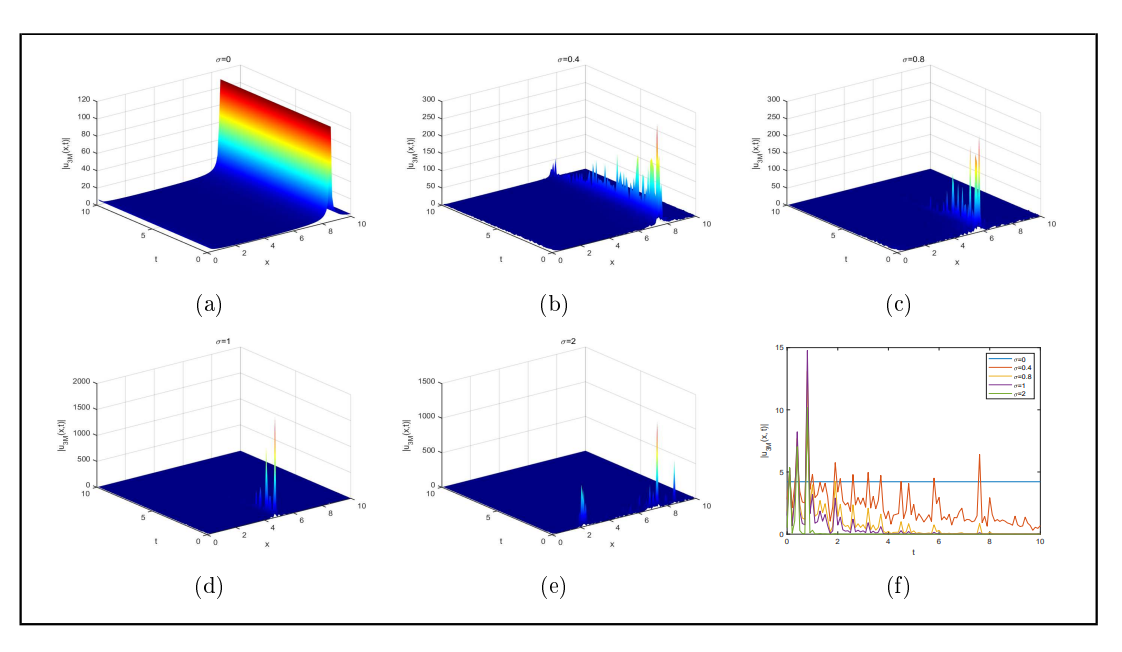
Ginzburg-Landau（金兹堡-朗道）方程是一种用于描述相变现象的数学模型，特别是在超导体和其他凝聚态物理系统中。这个方程由苏联著名物理学家维塔利·金斯堡（Vitaly Ginzburg）和列夫·朗道（Lev Landau）在1950年代初提出。历史上研究该方程为研究和设计超导材料和集成电路芯片提供了理论基础和工具，通过对相变和临界现象的深入理解，推动了这些领域的科学研究和技术应用。2024年，本团队的研究中的主要新颖性体现在以下五个方面：（1）对”分数阶导数”随机Ginzburg-Landau方程（FODSGLE）的研究提供了大量使用Jacobian椭圆函数（JEFs）的精确解。这些解为复杂物理现象提供了宝贵的见解，并在多个领域具有实际意义。（2）通过研究噪声对FODSGLE解的影响，我们发现无论”分数阶导数”的形式如何，解决方案的行为是一致的。随着噪声强度的增加，解的振幅下降并趋近于零。这项研究通过提供新的见解，超越了以往对FODSGLE动态理解的努力。（3）团队还研究了分数变化如何影响FODSGLE解中的噪声。令人惊讶的是，当噪声强度（$\sigma$）固定时，分数阶（$\alpha$）的变化对系统的影响最小。这揭示了现有文献中未被广泛探讨的一个方面。（4）团队在FODSGLE的背景下比较了不同类型的”分数阶导数”，提出了一项新颖的贡献，同时保持噪声强度或分数阶固定。我们的结果表明，相容分数阶与M截断”分数阶导数”的结果相近，而与使用贝塔分数阶获得的解存在更多差异。这一比较揭示了现有文献中未被深入研究的一个方面。（5）研究深入探讨了FODSGLE的相图，并研究了相关的敏感性和混沌行为。值得注意的是，之前关于随机Ginzburg-Landau方程（SGLE）的研究尚未广泛探讨这一方面。通过分析相图，我们对FODSGLE解的动态和稳定性获得了宝贵的见解，揭示了系统中的复杂行为。我们对敏感性和混沌行为的探索为理解FODSGLE提供了另一个维度，为该领域的进一步研究奠定了基础。该研究成果2024年发表于Fractals杂志.  https://doi.org/10.1142/S0218348X24501056期刊为中国科学院SCI3区杂志。作者顺序：孙逸群（第一作者），戚建明（唯一通讯作者），崔青华（我校研究生）。上海电机学院为唯一完成单位。

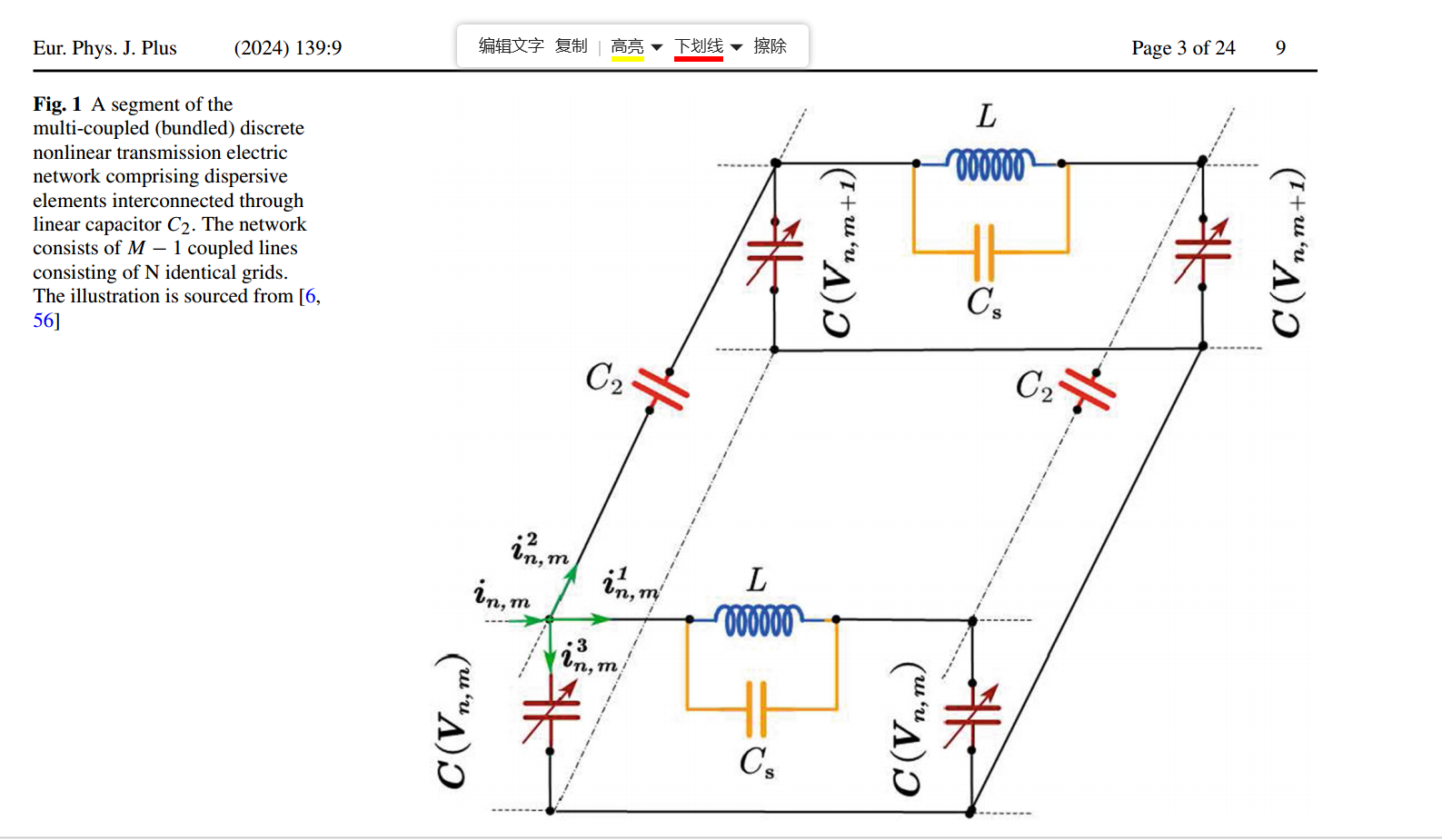
具有耗散元素的非线性电力传输网络模型中解结构的物理现象分析

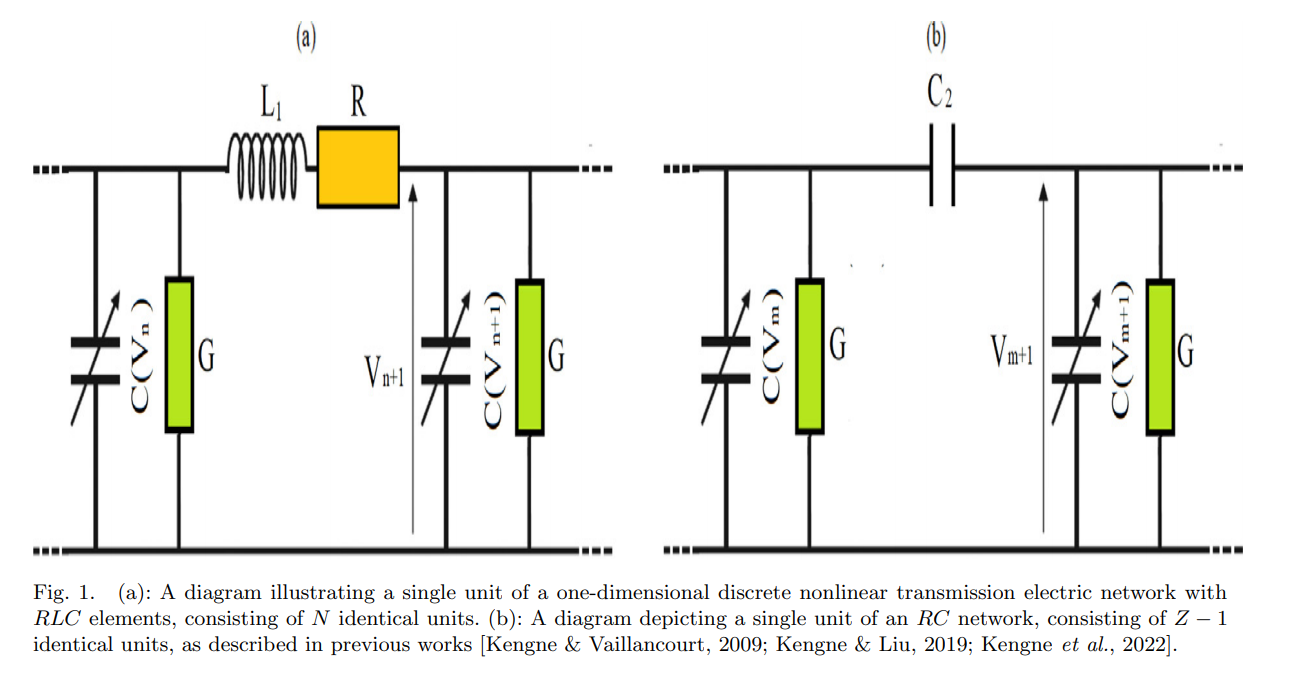
团队采用了一种新颖的方法来寻找多耦合离散非线性电力传输网络模型方程的精确解。在MATLAB R2021a软件的帮助下，研究提出了六个关键方面，这些方面体现了研究的创新性：（1）在本研究中，引入了($\frac{G'}{G^2}$)-展开法来探索多耦合离散非线性电力传输网络中模型电压方程的精确解。（2）首次探讨了”分数阶导数”在建模中的应用。由于”分数阶导数”能够捕捉记忆效应，因此可以更准确地描述电流和电压。（3）团队研究了分数阶对信号传输的影响，特别是对信号电压宽度、幅度和传播方向的影响。（4）基于前期文献的现有研究，团队首次探讨了色散元件Cs对传输电压的影响。我们的研究揭示了Cs引起电压幅度的变化，并对传输信号进行补偿，从而在确保稳定性和可靠性方面发挥了积极作用。（5）团队首次研究了通过改变斜率角$\theta$对非线性电力传输网络中电压方程精确解的变化。（6）本研究对非线性电力传输网络中由多种”分数阶导数”引起的电压变化进行了新颖的比较。我们的研究结果显示，不同”分数阶导数”之间的比较差异并不显著。我们使用图形模拟来研究上述（1）-（6）中不同参数对电压波形的影响。我们的分析揭示了电压波的传播受到分数阶、波斜率角以及其他相关物理参数的影响。

该研究成果2024年发表于 The European Physical Journal Plus  杂志

https://link.springer.com/article/10.1140/epjp/s13360-023-04736-1期刊为中国科学院SCI 3区杂志。作者顺序：白雷强（我校研究生）（第一作者），戚建明（唯一通讯作者），孙逸群。上海电机学院为唯一完成单位。

包含耗散元素的非线性电力传输网络模型中解结构的物理性质的研究

团队继续深入研究包含耗散元素的多耦合非线性传输网络中的电压方程。通过采用构造辅助方程法和运用”分数阶导数”的性质，探索了电流和电压的行为，考虑了记忆效应。该研究深入探讨了分数阶微积分对信号传输的影响，揭示了周期、幅度和传播方向的见解。此外，进一步分析了孤子传输斜率角和各种不同”分数阶导数”对电压波形的影响。稳定性分析表明，耗散元素和调制参数在信号稳定性和网络抗干扰能力方面发挥了重要作用。此外，团队还考察了自由参数对信号传输特性的影响。团队的研究结果突显了分数阶、波斜率和物理参数在电压传播中的复杂相互作用，填补了以往文献研究中的部分空白。该研究成果2024年发表于Physica Scripta杂志.  https://iopscience.iop.org/article/10.1088/1402-4896/ad5fce期刊为中国科学院SCI 3区杂志。作者顺序： 崔青华（我校研究生）（第一作者），孙逸群（唯一通讯作者），戚建明。上海电机学院为唯一完成单位。